

(Aquesta entrada participa a l'Edició 5.4 Martin Gardner del Carnaval de Matemáticas, l'amfitrió del qual és el blog Gaussianos.)
PRIMERA PART
 Hi ha un gran enrenou abans que comenci el Mundial de Futbol de Brasil 2014, ja que el Comitè Organitzador ha decidit introduir una modificació d'última hora.
Hi ha un gran enrenou abans que comenci el Mundial de Futbol de Brasil 2014, ja que el Comitè Organitzador ha decidit introduir una modificació d'última hora.
Volen aconseguir que participin més països que els 32 ja classificats per a la fase final del torneig. Hi han moltíssimes seleccions que han quedat fora del Campionat.
Donada l'enorme expectació que genera aquest Mundial, i la decepció de nombrosos països per no haver pogut classificar-se'n, els organitzadors del Mundial han decidit ampliar el nombre de seleccions que podran competir-hi.
Donada l'enorme expectació que genera aquest Mundial, i la decepció de nombrosos països per no haver pogut classificar-se'n, els organitzadors del Mundial han decidit ampliar el nombre de seleccions que podran competir-hi.
El calendari de competició establert inicialment per als 32 països era el següent: una primera ronda amb sistema de lliga amb 8 grups de 4 països, dels quals es classifiquen els 2 primers de cada grup.
Els 16 equips així classificats s'enfrontaran entre sí pel sistema d'eliminació directa fins a la final, a la qual el vencedor s'emportarà la Copa del Món.
No obstant això, si volen afegir més països, i que el campionat no es perllongui excessivament, han d'adoptar necessàriament un nou sistema de competició, descartant els grups inicials i realitzant partits eliminatoris des d'un principi.
A més, donada la disponibilitat dels diferents estadis de futbol i els problemes de logística, han determinat que, dels 64 partits que es preveia disputar amb l'antic sistema, com a màxim es podrien jugar 60 partits.
 El Comitè Organitzador ha arranjat una reunió amb diversos experts del Departament de Matemàtiques Aplicades del Ministeri d'Educació.
El Comitè Organitzador ha arranjat una reunió amb diversos experts del Departament de Matemàtiques Aplicades del Ministeri d'Educació.En aquesta reunió, el president del Comitè els hi explica a la resta d'assistents el parell de problemes que es presenten:
- El primer d'ells és determinar el nombre màxim de participants que hi pot haver si es celebren un total de 60 partits. Volem que vinguin la màxima quantitat possible de països. Així, d'una banda, tindrem més visites de turistes procedents dels països participants, i d'altra banda, tindrem més ingressos pels drets de televisió dels que decideixin veure’l des de casa.
- El segon és analitzar de quàntes formes diferents s'hi pot realitzar aquest torneig amb eliminatòries directes.
- A què et refereixes exactament?
- Vull dir que el campionat es pot disputar de moltes formes. Per exemple, pot haver 8 caps de sèrie, i que la resta de països competeixin entre ells fins que restin només 8 equips que s'enfrontin amb els caps de sèrie en vuitens de final. Així, si representem els partits a disputar com petits estadis rectangulars de color verd, i als equips participants amb una samarreta i un pantaló de futbol blau, l’esquema de competició quedaría d’aquesta forma:
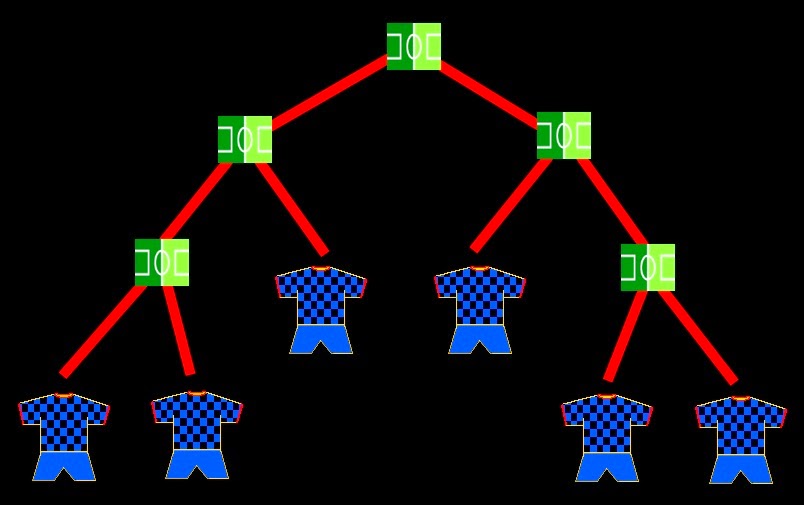
- O que hi hagi només 4 caps de sèrie, i que la resta s'eliminin fins que restin tan sols 4 seleccions que s'enfrontin amb ells.
- O que hi hagi tan sols 1 cap de sèrie (el país organitzador, és clar), i que la resta s'eliminin fins que quedi només un, que jugarà amb nosaltres la final. A la fi, totes les possibles variants que se us acudeixin.
- Entès. Però... no serà possible... És molta feina... per tan poc temps com resta.
- No vull excuses. Va, posem-nos mans a l'obra, i demà ens reunim novament aquí.
Després de la reunió, el cap del Departament de Matemàtiques Aplicades es mostra molt preocupat pels problemes plantejats. Voldries ajudar-lo?
SEGONA PART
Al dia següent, tornen a trobar-se'n els experts matemàtics i els membres del Comitè Organitzador.
- Anem-hi a intentar resoldre la primera qüestió. Què em dieu? Quin és el màxim nombre de països que podem convocar si es celebren 60 partits?
- Bé, crec que el millor serà confeccionar un quadre, com als tornejos de tennis. Representarem la final amb un petit camp de futbol, com vam dir anteriorment, i d'ell partiran 2 línies cap als dos equips que la disputaran. Ja tenim 1 partit.
- Ara substituïm les samarretes que representen els equips per altres dos camps de futbol, que representaran els 2 partits de semifinals. De cada un d'ells tornaran a partir 2 línies, cap als equips que les disputen. I si sumem aquests dos partits al partit de la final, ja comptem amb 3 partits en total.
- Seguim així amb els 4 partits de quarts de final, els 8 partits de vuitens de final, i els 16 partits de setzens de final. Ara tenim un total de 1+2+4+8+16 = 31 partits.
- Ens resten 29 partits per completar els 60 que volem que es disputin en el campionat. Així que no es poden celebrar tots els 32 partits de trenta-dosens de final, ja que tindríem un total de 31 + 32 = 63 partits. Podeu comptar els camps de futbol a l'esquema, per comprovar-hi que són 63.
- Ens sobren 3 partits. Així que eliminem 3 partits, fent que hi hagi 3 equips que es classifiquin directament per setzens de final.
- Ara comptem els equips que participaran al torneig: són les samarretes que pengen com fulles als extrems de cada branca.
- És veritat, l'esquema del torneig s'assembla a un arbre. Bé, després de comptar-los, em surten 61 samarretes, és a dir, que poden participar fins a 61 països, oi?
- És ben cert, sempre que el torneig s'organitzi amb aquest esquema de competició. Però, i si fem servir uns arbres diferents del que hem confeccionat? Si volem que hi hagi 8 caps de sèrie que comencin la seva participació en vuitens de final, o si volem que hi hagi 4 caps de sèrie, respetant sempre que siguin 60 partits els que es celebrin, els arbres serien els següents:
- Què passaria ara? Participarien d'aquesta forma més o menys països? I si se'ns ocorreixen altres arbres diferents dels que hem pintat?
- Doncs en aquests dos exemples són també 61 països, però no sé què passaria amb la resta d'arbres que puguem formar...
- Doncs en aquests dos exemples són també 61 països, però no sé què passaria amb la resta d'arbres que puguem formar...
- Sempre serien 61 països, encara que per demostrar-ho recorrerem a un procediment prou singular.
- Anem a comptar el països segons hi siguin eliminats i se'n vagin cap a casa. A tots els partits d'eliminació directa, hi haurà sempre un perdedor, que ja no jugarà més partits. Només hem de pensar que en 60 partits hi haurà 60 països 'perdedors', als quals haurem de sumar el que guanyi la final, que també se n'anirà a casa, però més content. Per tant, sempre hi haurà 61 països, independentment de la forma que adopti el calendari de competició.
- O podem veure-ho d'una altra forma: si en cada partit que hem representat amb un camp de futbol, pensem que l'equip que guanya l'encontre i passa a la següent fase ocupa la meitat més fosca, mentre que el perdedor ocupa la meitat pintada amb verd més clar, podem comprovar que en 60 partits hi han 60 meitats més clares, corresponents als 60 equips eliminats, als quals cal sumar l'equip que ha guanyat el torneig, i que sempre ha ocupat la zona fosca del camp. En total, 61 equips. I donarà el mateix l’arbre de competició que formem.
- A més, si encara no ho veieu massa clar, podéu veure el fenomenal article: Cuántos partidos hay en un torneo de tenis? de José Cárlos Gámez a Matemáticas Digitales.
- Doncs és veritat. Així que ja podem donar per resolt el primer problema d'esbrinar el màxim nombre de països que poden participar.
- Ara anem a veure la segona qüestió: veure de quàntes formes diferents s'hi pot organitzar el campionat. Dit d'una altra manera, hem d'avaluar els diferents arbres que podem confeccionar per organitzar el campionat amb 61 països.
- Bé, no sembla molt difícil. Anem a començar amb un campionat sense equips. No n’hi ha cap forma d’organitzar un campionat amb zero equips, oi?
- Ara pensem en un campionat amb un sol equip. És molt fácil. Tan sols hi ha una forma de fer-ho: li donem el trofeig a l’equip, i ja hi som.
- Amb 2 equips, tots dos jugarien la final, i ja hi és. Només hi hauria una forma d'organitzar-lo.
- Correcte.
- Amb 3 equips, també només hi ha una forma possible d'organitzar l'esdeveniment: primerament s'enfronten 2 equips entre si, i després el guanyador juga amb el tercer equip, no?
- Efectivament. Però, si en comptes d'enfrontar en primera ronda al primer equip amb el segon, fem que s'enfrontin el primer amb el tercer, o el segon amb el tercer, llavors tindriem altres 2 esquemes de competició diferents, no?
- No. És cert que els equips que s'enfrontarien serien diferents, però l'esquema de competició seria el mateix: primerament juguen dos, i el vencedor juga amb l'equip restant. De moment, el que ens interessa és esbrinar quants esquemes diferents es poden confeccionar i decidir-nos per un d’ells. Després ja veurem la forma de col·locar a cadascuna de les seleccions dins d’aquest esquema, d'acord? Així que els seguim pintant del mateix color a tots els equips, ja que no els volem diferenciar.
- Perfecte. Ara treballarem amb 4 equips. El més normal és fer que s'enfrontin entre ells en 2 semifinals, i que els guanyadors passin a la final.
- Però existeix una altra manera d'enfrontar-los, eliminant-se d'un en un.
- Així que, amb 4 equips, tenim 2 arbres diferents. Anem a veure amb 5 equips: hi ha 3 possibles maneres.
- Amb 7 equips podem formar 11 arbres diferents. Amb 8 hem construit 23 arbres i amb 9 podem disenyar 46 arbres. Però cada cop resulta més difícil dibuixar les diferents opcions. Crec que d'aquesta forma no arribarem enlloc...
- Potser hauriem de trobar alguna formula per a calcular quants arbres diferents es poden formar amb 61 competidors. Per això, estudiarem la sèrie que portem fins ara per veure si podem deduir quins seran els següents termes.
- Doncs no sembla pas que els nombres obtinguts segueixin cap tipus de seqüència matemática. Potser hauriem de buscar a l’internet una solución pel nostre problema.
- Sí, però el primer que hem de fer és definir exactament què és el que busquem.
 - Bé, aquests arbres que estem dibuixant s’anomenen ‘grafs’ en termes matemàtics. I com tenen una forma jeràrquica que s’assembla a la d'un arbre (o d'una arrel), també en matemàtiques se’ls coneix perl nom d’arbres.
- Bé, aquests arbres que estem dibuixant s’anomenen ‘grafs’ en termes matemàtics. I com tenen una forma jeràrquica que s’assembla a la d'un arbre (o d'una arrel), també en matemàtiques se’ls coneix perl nom d’arbres.
- A més, són uns arbres molt especials, ja que de tots els petits estadis (que anomenarem nodes) que representen els partits, parteixen 2 línies (branques o fills). No hi por haver un partit al què s’enfrontin més de 2 equips, així que parlarem d'arbres binaris, ni tampoc es pot jugar un partit amb un sol equip, per tant, diem que es tracta d’arbres estrictament binaris.
- Per altra banda, no ens importa l’ordre de les diferents branques, ja que ens hi fixem en l’estructura de l’arbre, i ens és igual de moment qui jugui els partits, com ja hem dit abans. Així que estem parlant d’arbres estrictament binaris no ordenats.
- Ja només cal utilitzar el cercador d’internet, posar ‘quants arbres estrictament binaris no ordenats es poden formar’ i esperar els resultats...

- Doncs no hi han molts resultats. A més, no em sembla que s'hi ajustin prou al que estem buscant. O potser no estem enfocant correctament el problema.
- Hauriem de reprendre novament la sèrie d’arbres que haviem calculat prèviament:
0 1 1 1 2 3 6 11 23 46 98
- I la introduirem en aquesta utilíssima pàgina web, que reconeix tota mena de sèries a partir dels seus termes:
 - Ahà! Aquí tenim la solució: es tracta de la sèrie A001190 de Wedderburn-Etherington. Podem comprovar que, entre les utilitats descrites per aquesta sèrie, trobem la de calcular el nombre de possibles calendaris de competició diferents que es poden formar amb un nombre determinat de participants.
- Ahà! Aquí tenim la solució: es tracta de la sèrie A001190 de Wedderburn-Etherington. Podem comprovar que, entre les utilitats descrites per aquesta sèrie, trobem la de calcular el nombre de possibles calendaris de competició diferents que es poden formar amb un nombre determinat de participants.
- Ara només hem de clicar a l’enllaç on T. D. Noe elabora una taula amb els 200 primers termes de la sèrie, i obtenir el resultat corresponent a 61 equips:
844206159208807054529
- Deu n’hi do! Quin nombre! Li posarem els punts, per tal de fer-nos una idea més precisa de la seva grandària.
844.206.159.208.807.054.529
- Més de 844 trilions d’arbres diferents! Ni a la selva amazònica n'hi han tants d'arbres!
 - Sembla un nombre prou gran. I vam dir que hauriem d’estudiar tots el casos per veure quin sistema adoptem, oi? Em sembla que haurem de treballar les 24 hores.
- Sembla un nombre prou gran. I vam dir que hauriem d’estudiar tots el casos per veure quin sistema adoptem, oi? Em sembla que haurem de treballar les 24 hores.
- Bé, pensem-hi una mica. Si un/una de nosaltres li dedica 1 minut a cada arbre, i no menja, ni dorm, ni descansa, necessitarà un total de 160.617.610.995.447 anys.
- Caldrà posar a treballar a tot el Departament.
- Què va, encara que tots el brasilers (més de 201 milions de persones) ens ajudessin en aquesta tasca, trigariem 7.989.625 anys en aconseguir-la.
- Bé, com que a gairebé totom li agrada el futbol, què tal si demanessim l’ajut de tota la població mundial?
- En aquest cas, tan sols es trigarien 221.987 anys per estudiar durant 1 sol minut cadascuna de les possibles formes d'organitzar el nostre campionat de 61 equips.
- Per cert, suposo que te'n recordes de quan vaig comentar que no ens interessava diferenciar els distints equips, i que haviem de centrar-nos tan sol en l'estructura del campionat, veritat?
- Sí, encara que no vaig entendre molt bé per què.
- Anem a retomar el tema per un moment. Tenim 61 equips, així que volem saber les distintes formes en que podem ordenar-los. En Matemàtiques, parlem de les permutacions que es poden donar en un conjunt de 61 elements.
- Això és. I és fàcil de calcular-les. El primer equip que triem pot ser qualsevulla de les 61 seleccions. Per a cada una d'elles, el segon equip l'agafarem aquesta vegada entre les 60 restants. Per a cada una d'aquestes combinacions de 2 equips, tindrem ara 59 equips entre els que triar el tercer païs. I així successivament.
- Per tant, el nombre total de permutacions dels 61 països serà igual a:
- Per cert, suposo que te'n recordes de quan vaig comentar que no ens interessava diferenciar els distints equips, i que haviem de centrar-nos tan sol en l'estructura del campionat, veritat?
- Sí, encara que no vaig entendre molt bé per què.
- Anem a retomar el tema per un moment. Tenim 61 equips, així que volem saber les distintes formes en que podem ordenar-los. En Matemàtiques, parlem de les permutacions que es poden donar en un conjunt de 61 elements.
- Això és. I és fàcil de calcular-les. El primer equip que triem pot ser qualsevulla de les 61 seleccions. Per a cada una d'elles, el segon equip l'agafarem aquesta vegada entre les 60 restants. Per a cada una d'aquestes combinacions de 2 equips, tindrem ara 59 equips entre els que triar el tercer païs. I així successivament.
- Per tant, el nombre total de permutacions dels 61 països serà igual a:
61 · 60 · 59 · 58 · ..... · 3 · 2 ·1 = 61!
- Efectivament, per abreujar utilitzem l'expressió 'factorial de 61', que representem amb el símbol d'admiració. I si fem el càlcul, obtindrem el següent resultat:
61! = 5,0758 · 10 83
- O sigui, un cinc seguit de 83 xifres més. Si el nombre d'arbres ja et semblava enorme (8,4421 · 10 20), imagina't com serà aquest. I si multipliquem el nombre d'arbres pel de les formes d'ordenar els distints països dins d'ells, obtindrem un preciòs nombre:
- Quaranta i dos mil vuitcents cinquanta gúgols de formes distints d'organitzar el nostre campionat! Hem de recordar que un googol es més gran que el nombre d'àtoms d'hidrògen que existeixen a l'univers conegut...
- Uff. Llavors crec que el millor será emprar el sistema tradicional: 29 partits de trenta-dosens, lliurant a tres països d’aquesta primera ronda, i eliminatòries completes des de setzens.
4,2850 · 10 104 = 42.850 · 10 100
- Quaranta i dos mil vuitcents cinquanta gúgols de formes distints d'organitzar el nostre campionat! Hem de recordar que un googol es més gran que el nombre d'àtoms d'hidrògen que existeixen a l'univers conegut...
- Uff. Llavors crec que el millor será emprar el sistema tradicional: 29 partits de trenta-dosens, lliurant a tres països d’aquesta primera ronda, i eliminatòries completes des de setzens.
- Els 3 països exents serien Brasil, i altres dos.
- És clar!
- Anem-hi! Ara toca decidir quins països convidem a participar al Mundial, per completar el quadre de 61 equips. I també hauriem de pensar en organitzar quelcom original per a la cerimònia d'apertura Què us aseembla si donem uns balons que omplin tot l'estadi?
- D'acord. Però abans, si algú està interessat en aquest tema de les estructures arbòries, aquí us deixo uns enllaços per aprofundir en ell: Matemáticas para computadora, Estructuras de datos, Árboles.
- Y més abaix us deixo altres enllaços, per si us ha agradat aquesta història i voleu compartir-la amb els vostres amics.
- Adeu siau. I que guanyi el millor!



































Cap comentari :
Publica un comentari a l'entrada