

(Aquesta entrada participa a la Edició 5.2. Emmy Noether del Carnaval de Matemàtiques, l'amfitrió del qual és el blog Mates de David.)
PRIMERA PART
 Surt el sol a una preciosa illa del Sud del Pacífic. És un lloc tan allunyat de qualsevol altre lloc habitat, que ni tan sols arriba el senyal telefònic per connectar-se'n a internet.
Surt el sol a una preciosa illa del Sud del Pacífic. És un lloc tan allunyat de qualsevol altre lloc habitat, que ni tan sols arriba el senyal telefònic per connectar-se'n a internet.
Tan sols cada dues hores passa per sobre un satèl·lit de telecomunicacions, que permet als seus habitants connectar-se amb la resta del món durant gairebé un minut.
Michael Laudrup ha escollit aquest idíl·lic lloc per passar unes tranquil·les i merescudes vacances amb la seva família.
Com cada matí, s'ha acostat a la costa per presenciar la bella matinada. Són les vuit del matí. Just en aquest moment passa per sobre el satèl·lit, i el telèfon sona indicant-li que té un missatge.
 No li ve de gust agafar el telèfon, però veu que es tracta d'un missatge del seu representant, així que finalment decideix llegir-lo. El missatge diu així:
No li ve de gust agafar el telèfon, però veu que es tracta d'un missatge del seu representant, així que finalment decideix llegir-lo. El missatge diu així:
'Michael, tens dues ofertes per entrenar la propera temporada. Una és de la Juventus de Torí, i l'altra és del Real Madrid. Com pots veure, uns t'ofereixen just el doble que els altres.
El problema és que necessiten una resposta immediata, així que d'aquí a 2 hores, quan tinguis novament connexió, hauràs contestar-me i dir-me per quin dels dos equips has decidit fitxar. Si no, tots dos buscaran un altre entrenador. La Juventus t'ofereix 2 milions d'euros, i el Real Madrid...'
Apa! Just en aquest moment, el satèl·lit s'havia allunyat prou com perquè es tallés la connexió.
 Michael tenia dues hores per a decidir per quin dels dos equips fitxar.
Michael tenia dues hores per a decidir per quin dels dos equips fitxar.Així que va baixar-hi fins a la platja, i va començar a meditar la resposta que li donaria al seu representant.
Ambdues ofertes procedien de dos equips amb els quals havia jugat, de manera que no sentia especial predilecció per l’un o l’altre.
L'oferta de la Juve és molt bona, però, i si la del Real Madrid és millor?
Serà una difícil elecció. Podria tirar sort, però es tracta d’una decisió important, què mereix buscar alguna forma lògica de prendre la decisió. Potser els coneixements de probabilitat que encara recordava dels seus estudis el podrien ajudar...
T'atreveixes a ajudar a Michael a escollir el seu nou equip per a la propera temporada?
SEGONA PART
Al principi, Laudrup pensa que l'oferta del Juventus és força temptadora. I a més, hi ha un 50% de probabilitat de que l'opció que triï sigui la millor de les dues.
 Ja m'agradaria guanyar aquests diners cada any... I atès que si tria l'oferta del Reial Madrid s'arrisca a guanyar menys diners, al cap de les dues hores jo contestaria: fitxo per la Juventus!
Ja m'agradaria guanyar aquests diners cada any... I atès que si tria l'oferta del Reial Madrid s'arrisca a guanyar menys diners, al cap de les dues hores jo contestaria: fitxo per la Juventus!Doncs sí, sembla una elecció lògica.
Sens dubte. Si canviant la seva elecció pot guanyar 2 milions, i tan sols pot perdre 1 milió, tot és ben clar, oi?
Bé, aquí estariem envers un estudi econòmic sobre la utilitat marginal d'aquests 2 milions: Laudrup pot ésser més preocupat per perdre 1 miliò, que interessat per guanyar 2 milions més.
Però suposarem que a Michael l'importa el mateix el milió adicional que pot guanyar que el que pot perdre, i abordarem el problema d'una altra forma. Vegem: tenim una oferta de 2.000.000 € de la Juventus, oi?
Però suposarem que a Michael l'importa el mateix el milió adicional que pot guanyar que el que pot perdre, i abordarem el problema d'una altra forma. Vegem: tenim una oferta de 2.000.000 € de la Juventus, oi?
Sí.
I sabem que una de les ofertes és el doble que l'altra. Així que el Real Madrid pot haver ofert 1 milió o 4 milions d'euros.
Correcte.
Bé, ara anem a calcular quin és el salari estimat que obtindrà Laudrup si canvia d'opinió i escull fitxar pel Real Madrid.
Hi ha un 50% de possibilitats de guanyar 1 milió d'euros, i un altre 50% de possibilitats de guanyar 4 milions d'euros. Així que el guany estimat d'aquesta segona opció, qué anomenarem E(Q2), la calcularem fent la mitjana dels dos casos que es poden donar:
Així que, si canvia d'opció, el seu guany mitjà s'estima en dos milions i mig, mig milió més que si es queda a l'equip de Torí, no?
Efectivament, si apliquem les lleis de la probabilitat, Laudrup hauria en aquest cas de triar la segona opció. Però a més, és un succès que no només passa en aquest cas, sinó que es donarà sempre que el representant expressi la diferència entre les dues ofertes en termes relatius.
No acabo de comprendre’n.
Anomenarem Qa i Qb a les dues ofertes. Definim r com la raó entre l’una i l’altra:
No ens importa quina de les dues ofertes, Qa o Qb, més gran. En tot cas, r sempre serà un nombre positiu més gran que zero (de moment, Laudrup no pensa entrenar cap equip de forma gratuïta, així que ni Qa ni Qb són iguals a zero, ni tampoc pensa pagar diners per fer-ho, així que Qa i Qb són dos valors positius majors que zero), i per tant, r també ho és.
Si fem que Q1 és l’oferta que triem en primer lloc, i Q2 és l’oferta que encara no hem descobert, tenim que Q2 pot valer (Q1 · r) o bé (Q1 / r).
Calculem el valor estimat de Q2, que anomenarem E(Q2), pel cas que hi ha la mateixa probabilitat de que qualsevulla de les dues ofertes sigui la més gran:
Si definim k com
Tenim que
Anem a veure gràficament com es comporta el valor de k en funció dels valors de r, és a dir, segons la diferencia que hi hagi entre les dues ofertes:

Veiem que k serà sempre més gran que 1, llevat del cas que les dues ofertes siguin iguals). de manera que el valor estimat de l'oferta desconeguda E(Q2) sempre serà més gran que el de l’oferta que coneixem Q1. Així que, sigui com sigui la primera opció, sempre haurem d'escollir la segona.
O sigui, que Laudrup haurà de contestar: fitxaré pel Real Madrid!
Sí, però... t’imagines què passaria si l’agent hagués citat en primer lloc l’oferta del Real Madrid? Tot i seguint el mateix raonament, ara Laudrup estaria pensant en fitxar per la Juve...
Malgrat això, tot això passa tan sols quan la relació entre ambdues ofertes l'expressem en termes relatius. Imaginem que el seu representant, en comptes de dir que una oferta és el doble que l'altra, hagués dit que una oferta és superior a l'altra en 1.000.000 € per exemple, és a dir, que hi hagués quantificat la diferència en valors absoluts. Què és el que passaria?
No ho sé.
Anem a calcular de nou el guany estimat de Laudrup si tria l’opció del Real Madrid:
Resulta que obtenim un guany estimat de 2.000.000 €, tot just la mateixa quantitat que li ofereix la Juventus!
Anem a veure-ho en termes matemàtics . Si ara definim r com:
tenim que:
Així que si la diferència la comptabilitzem en termes absoluts, i no relatius, passa que obtenim una solució matemàtica més 'lògica'...
És cert, en aquest cas el resultat matemàtic coincideix amb el que ens dicta el sentit comú.

I com les ofertes de tots dos clubs són iguals, i Laudrup té la mateixa simpatia per tots dos, li costaria molt decidir-se’n per un dels dos, pel qual Michael potser constestaría finalment: Em quedo al meu equip actual!
Bé, però aquestes oportunitats no sorgeixen cada dia. No podem ajudar-li d'alguna manera a decidir-se’n per una de les dues ofertes?
Està bé, després de tants càlculs, no li deixarem sense una solució pel seu problema.
Ja hem vist que segons interpretem les dades, la decisió pot ser diferent. Llavors, què ha de fer Laudrup per prendre una decisió correcta?

Te'n recordes de quan Llorente no sabia què fer, si fitxar pel Tottenham Hotspur o per l'Aston Villa? El vam veure fa un temps, a la nostra història ‘La difícil decisió de Llorente’.
Ah, sí, ja me'n recordo. En aquell cas el que havia de fer era aplicar la teoria de la parada òptima, oi?
Així és. El primer que ha de fer Laudrup és pensar quant vol guanyar per entrenar la temporada que ve, i si n’hi ha una oferta que iguali o superi aquesta quantitat, prendre-la, sense pensar que posteriorment pot tenir ofertes millors. I ja que en un principi l'oferta de la Juventus li semblava prou interessant i complia les seves expectatives, sens dubte hauria acceptar-la.

Llavors, podem concloure que Laudrup contestarà : Fitxo per la Juventus!
Ho sento, però tampoc serà així.
Com ? Hi ha algun raonament més que se'ns hagi escapat?
Sens dubte. Aquest problema que se li ha plantejat a Laudrup té una relació directa amb la teoria de la decisió i la interpretació bayesiana de la probabilitat, i ha estat estudiat des de fa temps per experts en lògica, filosofia, matemàtiques, etc. S'anomena la paradoxa dels dos sobres o paradoxa del canvi. En aquest enllaç, podràs trobar més informació sobre el tema: La paradoxa dels dos sobres: models del joc i simulacions.
Sí, però, al final, què és el que va fer Laudrup? Si no va fitxar pel Real Madrid, i tampoc per la Juve, què és el que va fer?
Efectivament, després de les 2 hores de passeig per la platja, va decidir que en cap dels dos llocs, ni a Madrid ni a Torí, podria veure les magnífiques matinades d'aquesta illa. I va decidir que tampoc tornaria a entrenar al seu equip actual. Es prendria un any sabàtic, descansant en aquest magnífic lloc amb la família.
I després d'enviar el missatge de resposta al seu representant, va fer el que havia d'haver fet quan va arribar a l'illa: apagar el telèfon.










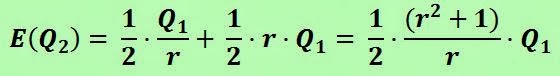

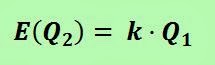








Cap comentari :
Publica un comentari a l'entrada